Model Matematika Sistem Kendali

Bab ini akan menyediakan pemodelan matematika sistem mekanik dan sistem listrik yang kita dapatkan dari pemodelan matematika rangkaian listrik sederhana dan sistem mekanik sederhana. Dalam bab ini kita mempertimbangkan pemodelan matematika dari berbagai sistem mekanik dan sistem listrik yang mungkin muncul dalam sistem kontrol

Hukum dasar yang mengatur sistem mekanik adalah hukum kedua Newton. pada bagian ini kami menerapkan hukum tersebut ke berbagai sistem mekanis dan menurunkan model transfer function.

Hukum dasar yang mengatur rangkaian listrik adalah hukum Kirchoff. Pada Bagian ini kita mendapatkan model Transfer-Function dari berbagai rangkaian listrik dan sistem penguat operasional yang mungkin  banyak muncul pada sistem kontrol.

Pemodelan matematika pada sistem mekanik

Bagian yang pertama ini membahas sistem pegas sederhana dan sistem peredam sederhana. Kemudian kami memperoleh model Transfer-Function dan model State-Space dari berbagai sistem mekanis.

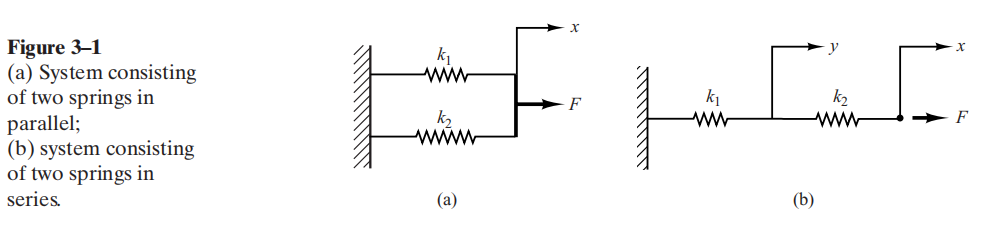
Mari kita dapatkan konstanta ekuivalen pegas untuk sistem yang masing-masing ditunjukkan pada Gambar (a) dan (b). Untuk pegas paralel [Gambar (a)] konstanta pegas ekuivalen k_eq diperoleh dari

atau

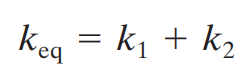
Untuk pegas yang tersusun secara seri [Gambar (b)] maka Gaya pada masing-masing pegas adalah sama, sehingga

Substitusikan persamaan y yang pertama ke dalam persamaan yang kedua sehingga menjadi

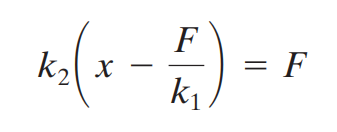
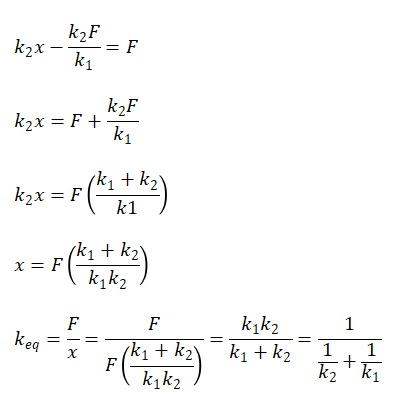
Mari kita dapatkan koefisien gesekan viskos yang setara untuk masing-masing sistem peredam yang ditunjukkan pada Gambar (a) dan (b). Peredam yang berisi minyak sering disebut dashpot. Dashpot adalah perangkat yang memberikan gesekan kental (gesekan viskos) atau redaman. Ini terdiri dari piston dan silinder berisi oli. Setiap gerakan relatif antara batang piston dan silinder ditahan oleh oli karena oli harus mengalir di sekitar piston (atau melalui lubang yang ada pada piston) dari satu sisi piston ke yang lain. Dashpot pada dasarnya menyerap energi. Energi yang diserap ini hilang sebagai panas, dan dashpot tidak menyimpan energi kinetik atau potensial

Mari kita dapatkan koefisien gesekan viskos yang setara untuk masing-masing sistem peredam yang ditunjukkan pada Gambar (a) dan (b). Peredam berisi minyak sering disebut dashpot. Dashpot adalah perangkat yang memberikan gesekan kental, atau redaman. Ini terdiri dari piston dan silinder berisi oli. Setiap gerakan relatif antara batang piston dan silinder ditahan oleh oli karena oli harus mengalir di sekitar piston (atau melalui lubang yang disediakan di piston) dari satu sisi piston ke sisi yang lain. Dashpot pada dasarnya menyerap energi. Energi yang diserap ini hilang sebagai panas, dan dashpot tidak menyimpan energi kinetik atau potensial

 

Pada Gambar (a) maka gaya F yang bekerja pada peredam adalah

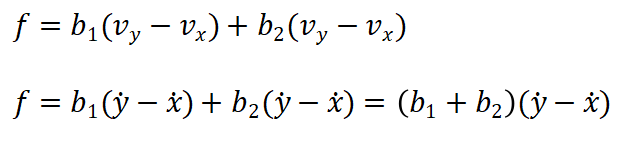
Dalam persamaan koefisien gesekan viskos maka gaya f  yang bekerja adalah

sehingga dapat diketahui bahwa


Pada gambar (b) maka gaya F yang bekerja pada peredam adalah

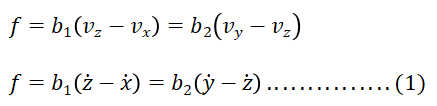
di mana z adalah perpindahan titik antara peredam b1 dan peredam b2 . (Perhatikan bahwa gaya yang sama ditransmisikan melalui poros.) Dari Persamaan (3-1), kita dapatkan

 

Atau

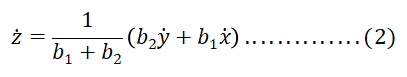
Dalam persamaan koefisien gesekan viskos b_eq, gaya f yang bekerja adalah

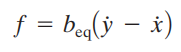
Dengan melakukan substitusi persamaan (2) ke persamaan (1) maka akan kita dapatkan 

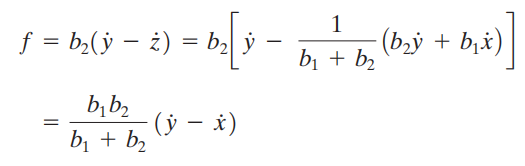
sehingga 

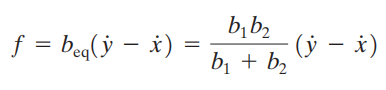
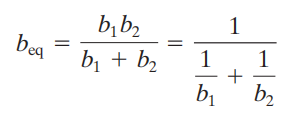
Diberikan suatu sistem spring-mass-dashpot yang dipasang pada gerobak tak bermassa seperti yang ditunjukkan pada Gambar di bawah ini

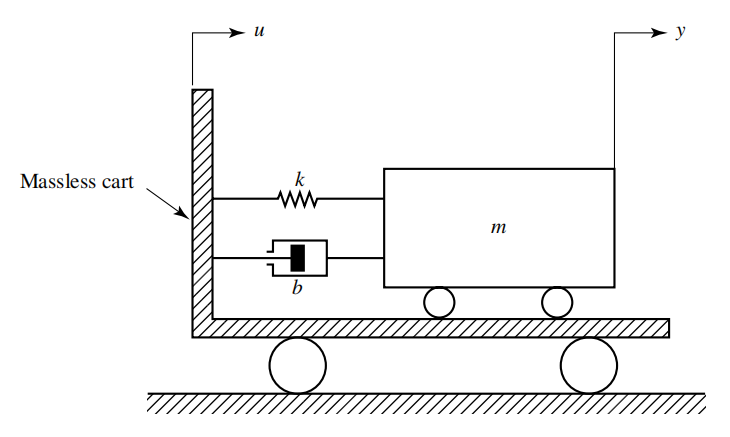
Mari kita peroleh model matematis dari sistem ini dengan mengasumsikan bahwa kereta berhenti selama t<0 dan sistem spring-mass-dashpot pada kereta juga diam selama t<0. Dalam sistem ini, u(t) adalah perpindahan kereta dan merupakan input sistem. Pada t=0, kereta bergerak dengan kecepatan konstan, atau konstan. Perpindahan y(t) dari massa adalah keluarannya. (Perpindahan relatif terhadap tanah.) Dalam sistem ini, m menunjukkan massa, b menunjukkan koefisien gesekan kental, dan k menunjukkan konstanta pegas. Kita asumsikan bahwa gaya gesekan dashpot sebanding dengan dan bahwa pegas adalah pegas linier, yaitu gaya pegas sebanding dengan y-u. Untuk sistem translasi, hukum kedua Newton menyatakan bahwa

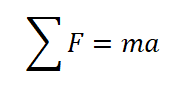
di mana m adalah massa, a adalah percepatan massa, dan ΣF adalah jumlah gaya yang bekerja pada massa dengan arah percepatan a. Menerapkan hukum Newton II ke sistem ini dan mencatat bahwa gerobak tidak bermassa, maka kita dapatkan persamaan :

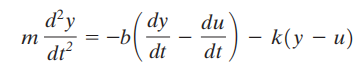
Persamaan ini mewakili model matematika dari sistem. dengan melakukan Transformasi Laplace dari persamaan terakhir ini, dengan asumsi kondisi awal nol maka :

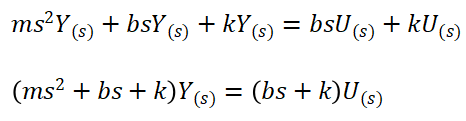
Dengan mengambil rasio Y(s) ke U(s), maka kita akan mendapatkan fungsi alih dari sistem tersebut menjadi

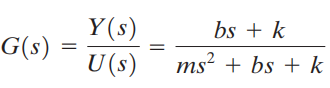
berikut video penjelasannya

Pemodelan matematika pada sistem elektrik

Hukum dasar yang mengatur rangkaian listrik adalah hukum arus dan hukum tegangan Kirchhoff. Hukum arus Kirchhoff (hukum node) menyatakan bahwa jumlah aljabar dari semua arus yang masuk dan keluar dari simpul adalah nol. (Hukum ini juga dapat dinyatakan sebagai berikut: Jumlah arus yang memasuki sebuah simpul sama dengan jumlah arus yang keluar dari simpul yang sama.) Hukum tegangan Kirchhoff (hukum loop) menyatakan bahwa pada saat tertentu jumlah aljabar tegangan di sekitar setiap loop dalam rangkaian listrik adalah nol. (Hukum ini juga dapat dinyatakan sebagai berikut:Jumlah penurunan tegangan sama dengan jumlah kenaikan tegangan di dalam loop tertutup.) Model matematika dari rangkaian listrik dapat diperoleh dengan menerapkan salah satu atau kedua hukum Kirchhoff.

Pada bagian ini kita akan membahas rangkaian listrik sederhana dan kemudian membahas pemodelan matematika dari sistem tersebut.

   

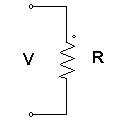
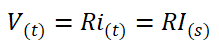
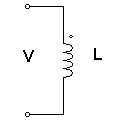
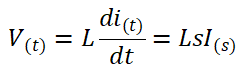
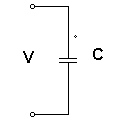
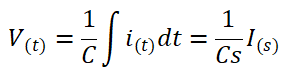
Pada sebuah rangkaian listrik yang ditunjukkan pada Gambar di bawah ini. 

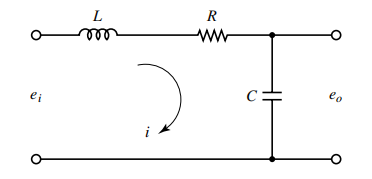
Rangkaian terdiri dari induktansi L (henry), resistansi R (ohm), dan kapasitansi C (farad). Dengan menerapkan hukum tegangan Kirchhoff ke sistem, maka dapat kita peroleh persamaan berikut:

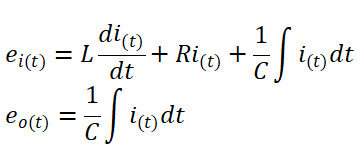
Fungsi alih pada persamaan dari rangkaian di atas dapat dilakukan dengan membawanya kedalam transformasi laplace, dengan asumsi kondisi awal nol. maka kita dapatkan persamaan :

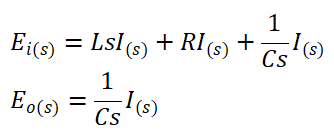
Jika e_i diasumsikan sebagai masukan dan e_o sebagai keluaran, maka fungsi alih dari sistem ini adalah

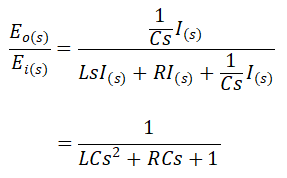
Fungsi Alih dari Rangkaian Seri-Paralel

Banyak sistem umpan balik memiliki komponen yang memuat satu sama lain. Perhatikan sistem yang ditunjukkan pada Gambar di bawah ini. Asumsikan ei adalah input dan eo adalah output. Kapasitansi C1 dan C2 pada awalnya tidak diisi

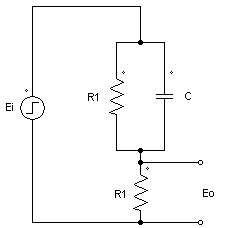
Analisa Rangkaian



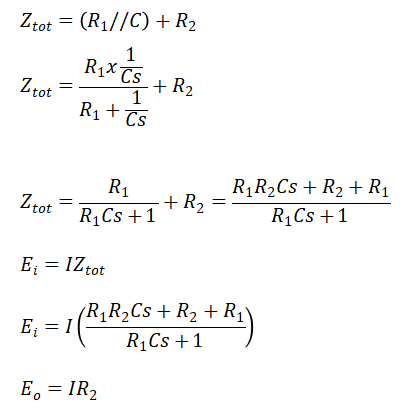
Sehingga Fungsi Alihnya adalah sebagai berikut:


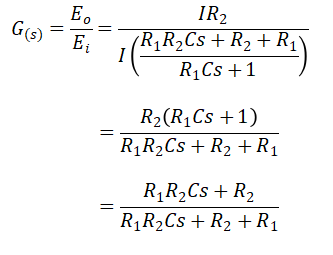
berikut video penjelasannya