PID Controller

Kontrol PID pada Plant. Gambar di bawah ini menunjukkan kontrol PID dari sebuah plant. Jika model matematis plant dapat diturunkan, maka dimungkinkan untuk menerapkan berbagai teknik desain untuk menentukan parameter pengontrol yang akan memenuhi spesifikasi transien dan kondisi tunak dari sistem loop tertutup. Namun, jika plant sangat rumit sehingga model matematisnya tidak dapat diperoleh dengan mudah, maka pendekatan analitik atau komputasi untuk merancang pengontrol PID tidak mungkin dilakukan. Kemudian kita harus menggunakan pendekatan eksperimental untuk penyetelan pengontrol PID.

 

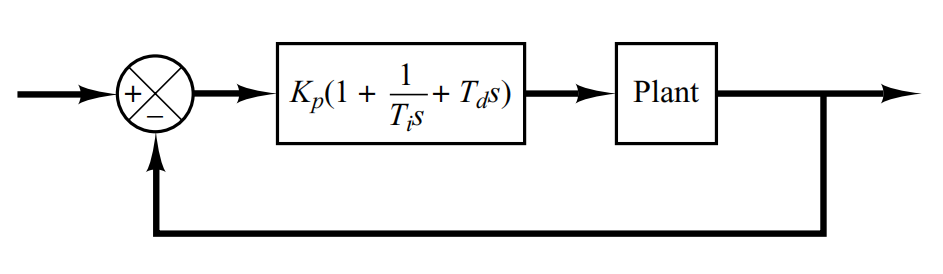
Proses pemilihan parameter pengontrol untuk memenuhi spesifikasi kinerja yang diberikan dikenal sebagai penyetelan pengontrol. Ziegler dan Nichols menyarankan aturan untuk menyetel pengontrol PID (artinya menyetel nilai dan ) berdasarkan respons langkah-langkah kontrol eksperimental atau berdasarkan nilai yang menghasilkan stabilitas marjinal ketika hanya tindakan proporsional yang digunakan. Aturan Ziegler-Nichols, yang disajikan secara singkat berikut ini, berguna ketika model matematika tumbuhan tidak diketahui. (Aturan-aturan ini tentu saja dapat diterapkan pada desain sistem dengan model matematika yang diketahui. Aturan seperti itu menyarankan seperangkat nilai dan yang akan memberikan operasi sistem yang stabil. Namun, sistem yang dihasilkan mungkin menunjukkan overshoot maksimum yang besar dalam respons langkah, yang tidak dapat diterima. Dalam kasus seperti itu kita membutuhkan serangkaian penyetelan halus sampai diperoleh hasil yang dapat diterima. Nyatanya, aturan penyetelan Ziegler–Nichols memberikan perkiraan terpelajar untuk nilai parameter dan memberikan titik awal untuk penyetelan halus, daripada memberikan setelan akhir untuk dan dalam satu jepretan.

Aturan Ziegler–Nichols untuk Menyetel Kontroler PID

Ziegler dan Nichols mengusulkan aturan untuk menentukan nilai waktu integral gain proporsional dan waktu turunan berdasarkan karakteristik respons transien dari plant tertentu. Penentuan parameter pengontrol PID atau penyetelan pengontrol PID dapat dilakukan oleh para insinyur di lokasi melalui eksperimen di pabrik. (Banyak aturan penyetelan untuk pengontrol PID telah diusulkan sejak proposal Ziegler–Nichols) Ada dua metode yang disebut aturan penyetelan Ziegler–Nichols: metode pertama dan metode kedua . Akan kita bahas pada pembahasan di bawah ini.

Metode Pertama. 

Dalam metode pertama, secara eksperimental kita memperoleh respon plat terhadap masukan unit-step, seperti yang ditunjukkan pada di bawah ini. Jika plant tidak melibatkan integrator(s) atau tiang konjugasi kompleks yang dominan, maka kurva respons unit-step seperti itu mungkin terlihat berbentuk S. Metode ini berlaku jika respons terhadap input step menunjukkan kurva berbentuk S. Kurva step-respon seperti itu dapat dihasilkan secara eksperimental atau dari simulasi dinamis pabrik.

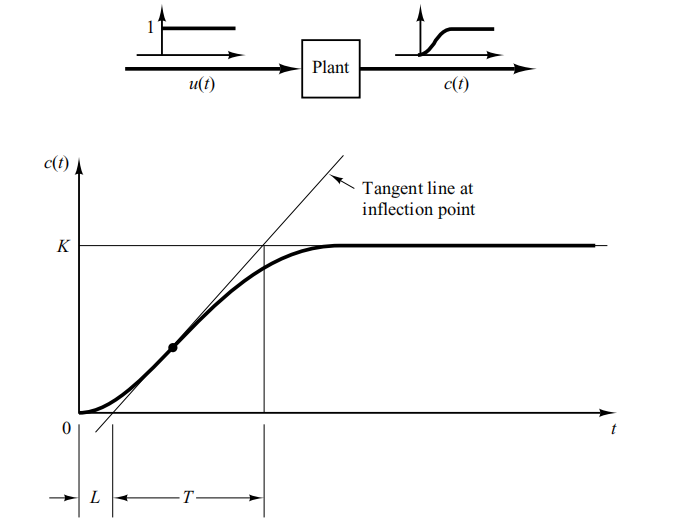
Kurva berbentuk S dapat dicirikan oleh dua konstanta, waktu tunda L dan konstanta waktu T. Waktu tunda dan konstanta waktu ditentukan dengan menggambar garis singgung pada titik belok kurva berbentuk S dan menentukan perpotongan garis singgung sejajar dengan sumbu waktu dan garis c(t)=K, seperti yang ditunjukkan pada gambar di atas. Fungsi transfer C(s)/U(s) kemudian dapat didekati dengan sistem orde pertama dengan lag transport sebagai berikut:

 

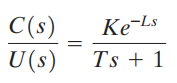
Ziegler dan Nichols menyarankan untuk menetapkan nilai dari dan menurut rumus yang ditunjukkan pada Tabel berikut:

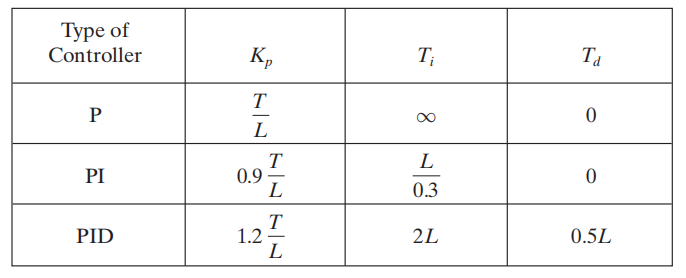
Perhatikan bahwa pengontrol PID disetel dengan metode pertama yang diberikan aturan Ziegler–Nichols

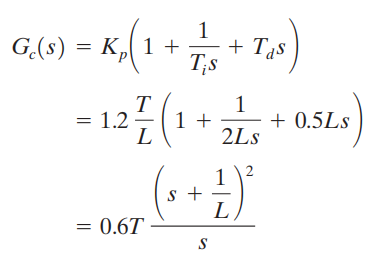
Dengan demikian, pengontrol PID memiliki kutub pada titik asal dan nol ganda pada s=–1/L.

Metode Kedua. 

Dalam metode kedua, pertama-tama kita menetapkan dan Menggunakan aksi kontrol proporsional saja, naikkan Kp dari 0 ke nilai kritis Kcr di mana output pertama kali menunjukkan osilasi berkelanjutan. (Jika output tidak menunjukkan osilasi berkelanjutan untuk nilai berapa pun yang diambil Kp, maka metode ini tidak berlaku.) Jadi, gain kritis Kcr dan periode yang sesuai ditentukan secara eksperimental.

 

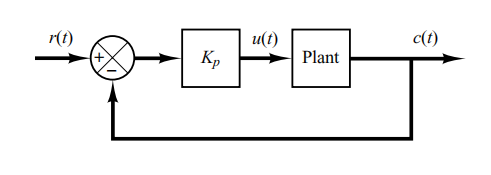
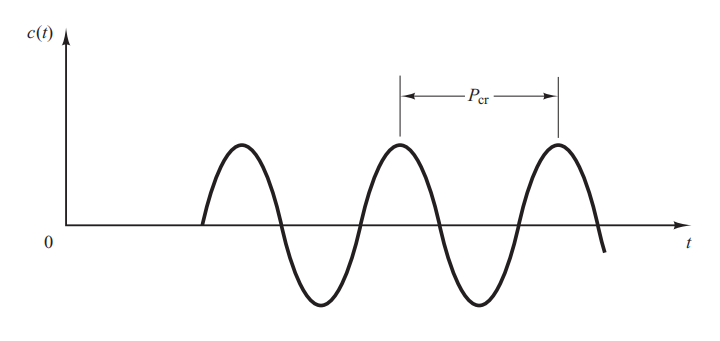
Perhatikan Ziegler dan Nichols menyarankan agar kita menetapkan nilai parameter (Kp, Ti, Td) dan menurut rumus yang ditunjukkan pada Tabel di bawah ini. 

Aturan Tuning Ziegler–Nichols Berdasarkan Kcr Gain Kritis dan Periode Kritis (Metode Kedua) Pcr

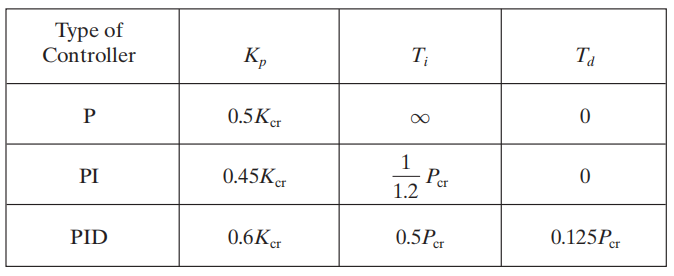
Perhatikan bahwa pengontrol PID disetel dengan metode kedua dari aturan Ziegler–Nichols

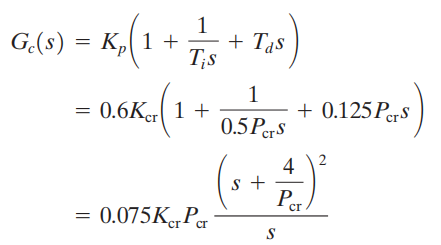
Perhatikan bahwa jika sistem memiliki model matematika yang diketahui (seperti fungsi transfer), maka kita dapat menggunakan metode root-locus untuk menemukan gain kritis Kcr dan frekuensi osilasi berkelanjutan cr, di mana

 

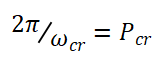
Nilai-nilai ini dapat ditemukan dari titik persilangan cabang-cabang root-lokus dengan sumbu jω(Jelas, jika cabang root-locus tidak melewati sumbu jω, metode ini tidak berlaku.)

Aturan metode Ziegler–Nichols telah digunakan secara luas untuk menyetel kontroler PID dalam sistem kontrol proses di mana dinamika plant tidak diketahui dengan tepat. Selama bertahun-tahun, aturan penyetelan seperti itu terbukti sangat berguna. Aturan penyetelan Ziegler–Nichols dapat, tentu saja, diterapkan pada Plant yang dinamikanya diketahui. (Jika dinamika plant diketahui, tersedia banyak pendekatan analitik dan grafis untuk desain pengontrol PID, selain aturan penyetelan Ziegler–Nichols.)

CONTOH

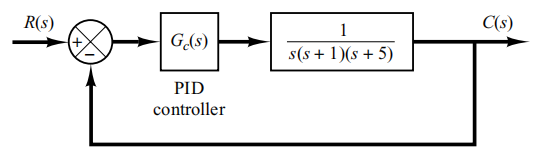
Perhatikan sistem kontrol yang ditunjukkan pada Gambar di bawah ini

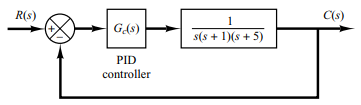
 Di mana kontroler PID digunakan untuk mengontrol sistem. Kontroler PID memiliki fungsi transfer

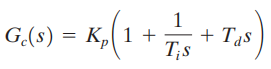
Meskipun banyak metode analitik tersedia untuk desain pengontrol PID untuk sistem ini, mari kita terapkan aturan penyetelan Ziegler–Nichols untuk penentuan nilai parameter dan Kemudian dapatkan kurva respons step-unit dan periksa untuk melihat apakah sistem yang dirancang menunjukkan sekitar 25% overshoot maksimum. Jika overshoot maksimum berlebihan (40% atau lebih), lakukan fine tuning dan kurangi jumlah overshoot maksimum hingga kira-kira 25% atau kurang

Karena plant memiliki integrator, maka kita gunakan metode kedua dari aturan penyetelan Ziegler-Nichols. Dengan mengatur Ti=∞ dan Td=0, maka kita peroleh fungsi transfer loop tertutup sebagai berikut:

 

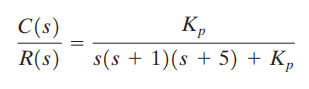
Nilai Kp yang membuat sistem sedikit stabil sehingga terjadi osilasi berkelanjutan dapat diperoleh dengan menggunakan kriteria stabilitas Routh. Karena persamaan karakteristik untuk sistem loop tertutup adalah

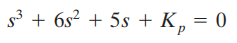
Routh Array-nya adalah sebagai berkut:

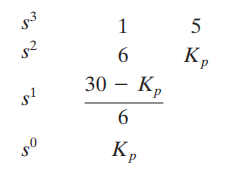
Memeriksa koefisien kolom pertama dari tabel Routh, kami menemukan bahwa osilasi berkelanjutan akan terjadi jika gain kritis Kcr adalah

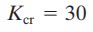
Dengan gain Kp ditetapkan sama dengan Kcr (=30), persamaan karakteristiknya menjadi

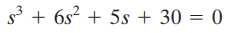
Untuk mencari frekuensi osilasi berkelanjutan, kita substitusikan s=jω ke dalam persamaan karakteristik ini sebagai berikut:

 

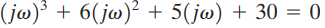
atau

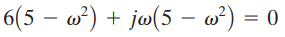
sehingga kita menemukan frekuensi osilasi berkelanjutan menjadiatau Jadi, periode getaran berkelanjutan adalah

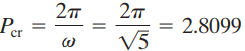
berdasarkan tabel penentuan Kp, Ki, Kd di atas maka dapat diperoleh 

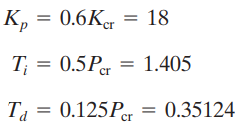
Adapun Fungsi Alih dari PID Controller adalah sebagai berikut

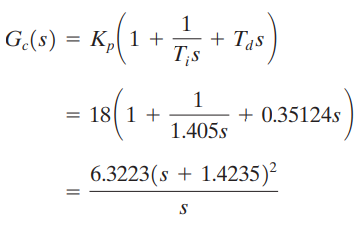
Controller PID memiliki sebuah pole di titik asal dan double-zero di 

Adapun blok diagram sistem dengan PID controller yang sudah didesain tadi dapat kita lihat pada gambar di bawah ini:

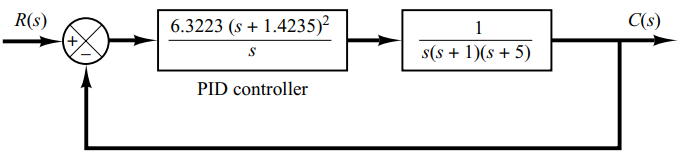
Contoh Soal:

Desainlah Controller PID untuk sistem berikut ini: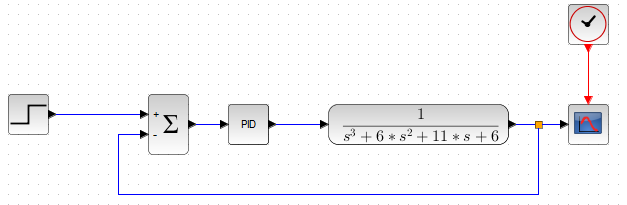

jika kita perhatikan bahwa transfer function sistem tersebut adalah

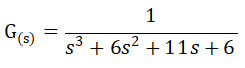
Sekarang coba kita simulasikan tanpa controller PID dengan menggunakan software Scilab.

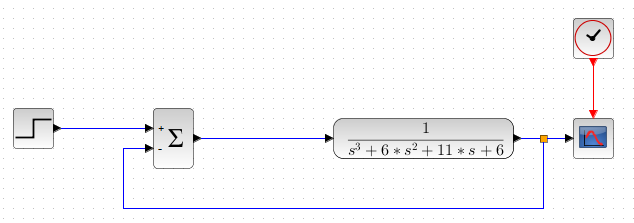
dan ini adalah hasil output responnya

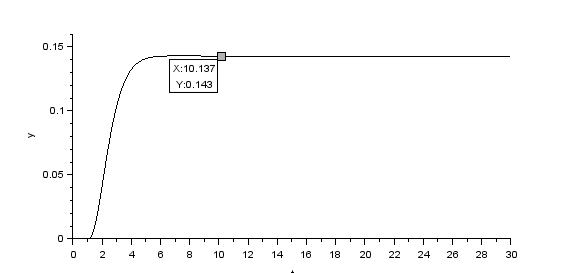
Perhatikan bahwa sistem tersebut steady di y=0,143 yang seharusnya steady di y=1, sehingga sistem ini memiliki steady state error sekitar 85,7% sehingga perlu adanya sistem pengendali untuk menekan error tersebut sekecil mungkin hingga mendekati 0%, salah satu caranya adalah dengan menggunakan PID Controller.
Hal pertama yang harus kita lakukan adalah dengan mencari Kcr dimana dengan Gain ini maka sistem akan berada pada kondisi kritis yang menyebabkan respon sistem berosilasi secara terus-menerus. penambahan Kp akan menyebabkan Fungsi alih menjadi seperti di bawah ini:

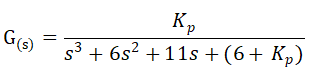
Routh-Hourwitz adalah salah satu metode yang sangat mudah dan cepat untuk menentukan nilai Kcr

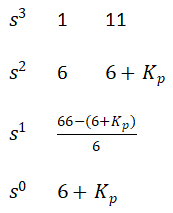
sehingga nilai Kcr adalah 

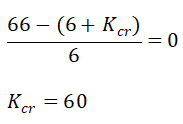
dan berikut hasil simulasinya


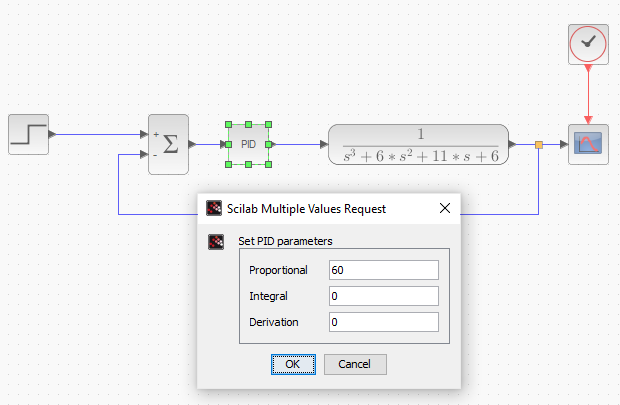
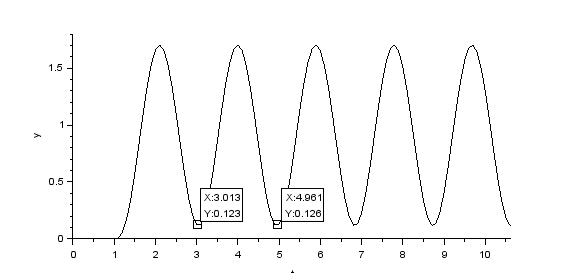
Dapat dilihat bahwa sistem mencapai kondisi kritis ketika Kp=Kcr=60 dengan Periode (Pcr)=4,961-3,013=1,948s sehingga dapat didapatkan parameter Kp, Ki, Kd sebagai berikut :

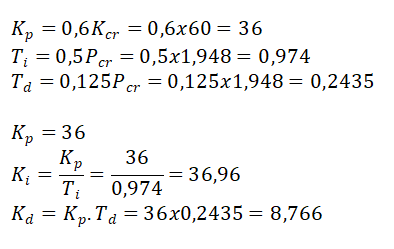
dan berikut hasil simulasinya


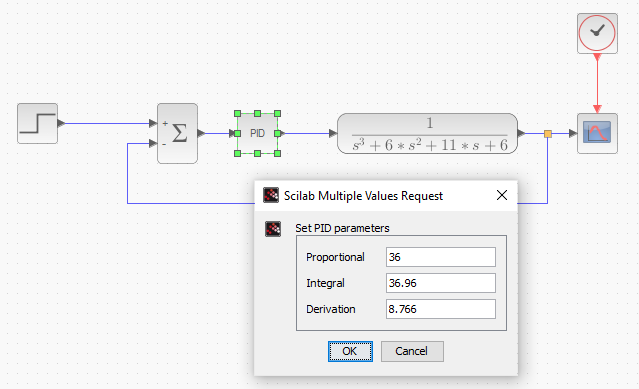
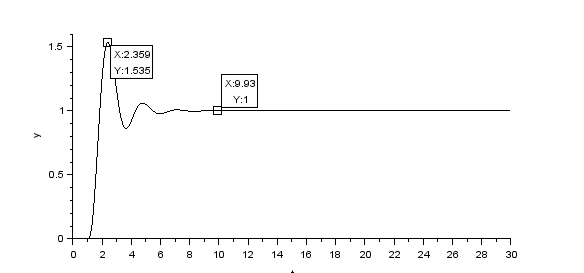
Namun output respon tersebut masih memiliki Maksimum Overshoot yang cukup tinggi yaitu 53,5% lebih tinggi dari setpoint sehingga untuk mendapatkan output respon yang lebih baik maka perlu dilakukan fine-tuning secara manual.
dan berikut output respon setelah dilakukan fine-tuning


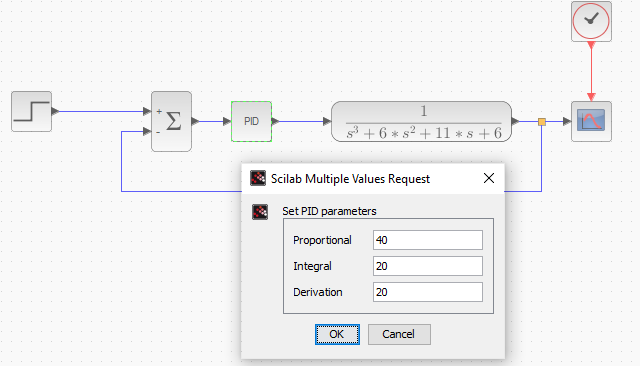
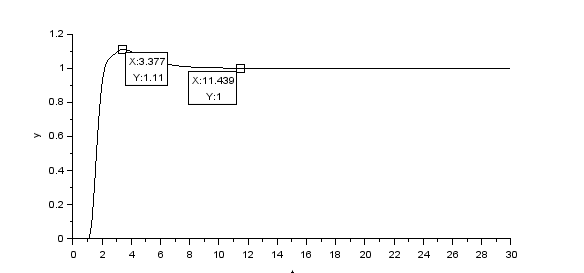
dapat dilihat bahwa setelah dilakukan fine tuning maka Maximum-Overshoot dapat ditekan menjadi sekitar 11% dan tidak terjadi osilasi adapun steady-state errornya adalah 0% karena pada kondisi steady nilai output yang dihasilkan sama dengan setpoint yang diinginkan.